En esta oportunidad, mediante el empleo del solver determinaremos el uso óptimo de recursos para una fábrica de productos químicos. El ejercicio es el siguiente:
- Alchemist Inc., fabrica dos tipos de productos químicos, E y F, cuya utilidad neta es de $5000 y $4000 por tonelada respectivamente.
- Ambos pasan por operaciones de 2 departamentos de producción, que tienen una disponibilidad limitada.
- El departamento A dispone de 150 horas mensuales; cada tonelada de E utiliza 10 horas de este departamento, y cada tonelada de F, 15 horas.
- El departamento B tiene una disponibilidad de 160 horas mensuales. Cada tonelada de E precisa de 20 horas, y cada tonelada de F precisa de 10 horas para su producción.
- Para la producción global de E y F, se deberán utilizar al menos 135 horas de verificación en el próximo mes; el producto E precisa de 30 horas y F de 10 horas por tonelada de verificación .
- La alta gerencia ha decretado que es necesario producir al menos una tonelada de F por cada 3 de E .
- Un cliente ha solicitado 5 toneladas, cualquiera sea su tipo, de E o F.
- Por otro lado, es evidente que no pueden producirse cantidades negativas de E ni de F.
Se trata de decidir, para el mes próximo, las cantidades a producir de cada uno de los productos para maximizar la utilidad global.
El Modelo
Variables controlables
E : toneladas de tipo E a producir;
F: toneladas de tipo F a producir;
Modelo:
Max 5000 E +4000 F {Función objetivo: maximizar la utilidad global}
sujeto a
10 E +15 F£ 150 {horas del departamento A}
20 E +10 F£ 160 {horas del departamento B}
30 E +10 F³ 135 {horas de verificación}
E -3 F£ 0 {al menos una de F cada 3 E significa E £ 3 F}
E + F ³ 5 {al menos 5 toneladas}
E ³ 0, F ³ 0 {no negatividad}
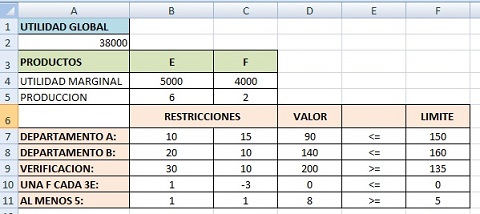
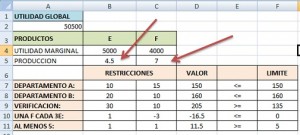
Antes de introducir este modelo en la planilla, conviene preparar una tabla con los coeficientes de las variables:
| Productos: | E | F | ||
| Utilidad marginal: | 5000 | 4000 | ||
| Restricciones | ||||
| Departamento A: | 10 | 15 | £ | 150 |
| Departamento B: | 20 | 10 | £ | 160 |
| Verificación: | 30 | 10 | ³ | 135 |
| Al menos un E cada 3F: | 1 | -3 | £ | 0 |
| Al menos 5: | 1 | 1 | ³ | 5 |
Las restricciones de no negatividad no las hemos incluido en la tabla, pero sí las tendremos muy en cuenta al poner restricciones en la planilla. De otro modo, podríamos llegar a obtener soluciones absurdas.
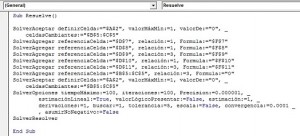
En el visual basic, solver aparecería de la siguiente manera:
(Para una mayor visualización de la imagen, hacer click en la misma)
Sub Resuelve()
SolverAceptar definirCelda:="$A$2", valorMáxMín:=1, valorDe:="0", celdasCambiantes:="$B$5:$C$5"
SolverAgregar referenciaCelda:="$D$7", relación:=1, Formula:="$F$7"
SolverAgregar referenciaCelda:="$D$8", relación:=1, Formula:="$F$8"
SolverAgregar referenciaCelda:="$D$9", relación:=3, Formula:="$F$9"
SolverAgregar referenciaCelda:="$D$10", relación:=1, Formula:="$F$10"
SolverAgregar referenciaCelda:="$D$11", relación:=3, Formula:="$F$11"
SolverAgregar referenciaCelda:="$B$5:$C$5", relación:=3, Formula:="0"
SolverAceptar definirCelda:="$A$2", valorMáxMín:=1, valorDe:="0", celdasCambiantes:="$B$5:$C$5"
SolverOpciones tiempoMáximo:=100, iteraciones:=100, Precision:=0.000001, estimaciónLineal:=True, valorLógicoPresentar:=False, estimación:=1, derivaciones:=1, buscar:=1, tolerancia:=5, escala:=False, convergencia:=0.0001 , asumirNoNegativo:=False
SolverResolver
End Sub
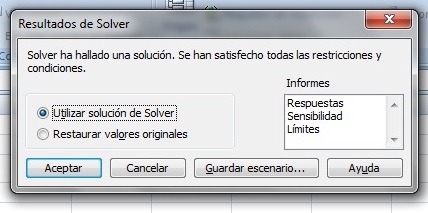
Solver arrojará el siguiente resultado respecto al óptimo uso de los recursos:
Elaborado por: Sara Ramos

08/10/2012 a las 7:13 am
Es un material bueno, felicitaciones.
Esteré en contacto para algunos comentarios o sugerencias posteriores.
Saludos.
06/12/2014 a las 7:00 am
como puedo ver el procedimiento :
solverResolver
SolverAgregar
etc...?
12/11/2015 a las 12:37 pm
Quiero saber el procedimiento.... para resolver problemas con solver!!!
10/06/2017 a las 4:25 pm
la macro con solver, a la linea "valorde:=" puede ponerse como referencia una celda o como se podria hacer. Estoy buscando que capte un valor de una celda que es definido por le usuario.