La función WorksheetFunction.Binom_Dist sirve obtener la probabilidad de una variable discreta siguiendo una distribución de tipo binomial.
Nota: Con distribución binomial nos referimos a que el resultado de un ensayo puede ser solo entre éxito o fracaso. Usualmente para la probabilidad de estos se usa "p" y "q" respectivamente, siendo "q=1-p".
Sintaxis de la función:
WorksheetFunction.Binom_Dist(Arg1, arg2, Arg3, Arg4)
Nombre Obligatorio Tipo de dato Descripción
Arg1 Obligatorio Double El número de éxitos en los ensayos.
Arg2 Obligatorio Double El número de ensayos independientes o muestras.
Arg3 Obligatorio Double Probabilidad de éxito en cada ensayo o muestra seleccionada
Arg4 Obligatorio Boolean TRUE: Devuelve la función de distribución acumulativa, que es la probabilidad de que haya un máximo de número de éxitos; FALSE: Devuelve la función de probabilidad bruta, que es la probabilidad de que haya número de éxitos.
A continuación, un ejemplo para entender la aplicación y reconocer los parámetros/argumentos de la función en VBA
Ejemplo:
Se tiene una máquina, la cual se conoce que el 18% de lo que produce es defectuoso.
Si analizamos una muestra de 10 elementos producidos entonces….
A. ¿Cuál es la probabilidad que 3 o menos sean defectuosos?
B. ¿Cuál es la probabilidad que exactamente los 3 sean defectuosos?
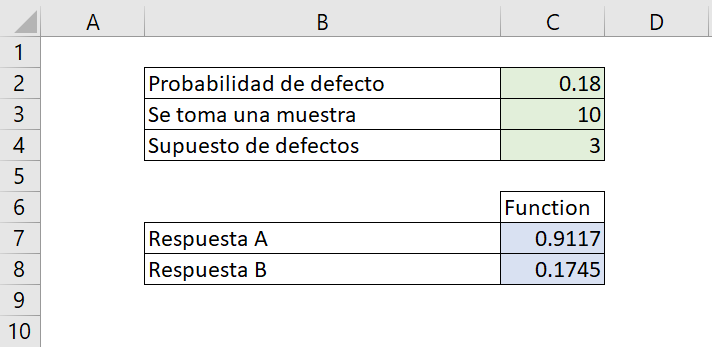
Para el resultado presentado en C7 y C8 se añade el código siguiente:
Sub prueba_PROB_BINOMIAL()
'sintaxis
'Application.WorksheetFunction.Binom_Dist( exitos, ensayos, prob.exito, acumulado(T) o Puntual(F))
prob_exito = Range("C2")
ensayos = Range("C3")
num_exitos = Range("C4")
Rptaacumulada = Application.WorksheetFunction.Binom_Dist(num_exitos, ensayos, prob_exito, True)
Rptaexacta = Application.WorksheetFunction.Binom_Dist(num_exitos, ensayos, prob_exito, False)
Range("C7") = Rptaacumulada
Range("C8") = Rptaexacta
End Sub
El programa calculó las probabilidades según los datos suministrados, para la primera respuesta "A", la probabilidad 0.9117 corresponde a la posibilidad de encontrar 3 o menos defectos, es decir 0 ,1 ,2 o 3 defectos, es por ello que se llama acumulada.
Para la respuesta "B", la probabilidad 0.1745 corresponde únicamente a la posibilidad que tendríamos de encontrar los 3 elementos en estado defectuoso.
Nota adicional: La respuesta "A" también la podemos obtener si hallamos la probabilidad puntual de:
0 defectuosos
1 defectuoso
2 defectuosos
3 defectuosos
Y sumáramos todas ellas, del siguiente modo:
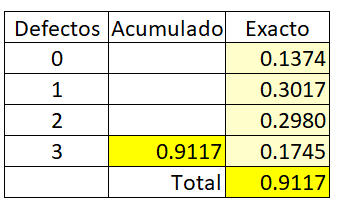
Se adjunta el archivo Excel con el ejemplo: WorksheetFunction.Binom_Dist VBA
Por: Alex Huaroc
