Uno de los problemas clásicos en microeconomía es hallar la maximización de utilidad del consumidor, para ello es necesario hallar las cantidades óptimas consumidas del individuo dada su restricción.
Para entender mejor el problema se puede realizar un ejemplo donde Y= Naranjas y X=Manzanas
Imaginando que la Utilidad del individuo presenta la siguiente forma:
Donde:
U : Utilidad que siente el individuo al consumir ambos bienes. Significa que tan feliz se siente al comer manzanas y naranjas.
alpha: Nivel de preferencia hacia el bien asociado. Dado que solo se consumen dos bienes, los niveles de preferencia asociados serán y Por ejemplo, si al individuo le gustan las manzanas tanto como le gustan las naranjas, entonces alpha=0.5=(1-alpha) y si le gustan las manzanas el triple de lo que le gustan las naranjas entonces: alpha=0.75 y (1-alpha)=0.25.
El individuo preferiría comer la mayor cantidad de manzanas y naranjas; sin embargo tiene una cantidad limitada de dinero para pagar por el precio de ambos bienes.
I: es el ingreso del individuo; es decir, de cuánto dinero dispone para comprar
P: Son el precio de las manzanas y las naranjas.
En base a estas ecuaciones se plantea un lagrangiano y se optimiza usando derivadas; sin embargo, lo importante es la lógica que tiene el resultado:
En el primer caso, interpretando según las variables que se mencionaron anteriormente se puede ver que: “La cantidad de manzanas que el individuo compra depende positivamente de cuánto dinero dispone y negativamente del precio de cada manzana”
Creamos la UDF para hallar el consumo óptimo:
Function CantidadOptimaConsumida(arg1, arg2, arg3)
Resultado = arg1 * arg2 / arg3
Utilidad = Resultado
MsgBox "La cantidad consumida del bien es " & Resultado
End Function
En la UDF creada, se interpretan los valores como:
Arg1=alpha, el nivel de preferencia asociado.
Arg2= I, el ingreso económico del que se dispone.
Arg3= P, el precio del bien que se desea consumir. para manzanas y para naranjas.
Para entender cómo funciona podemos aplicar unos ejemplos numéricos:
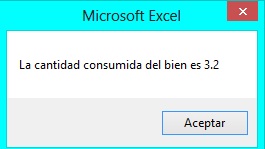
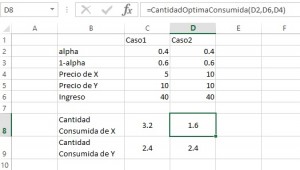
1) Hallar la cantidad de consumo óptima de manzanas si su preferencia asociada es 0.4, su precio es igual a S/.5 y se dispone de S/.40
Aplicamos la UDF, donde “arg1=0.4”, “arg2=40” y “arg3=5” y se obtiene como resultado:
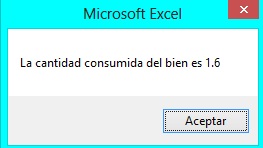
2) ¿Que sucede con la cantidad de consumo óptima si el precio de las manzanas se duplica?
Aplicamos la UDF nuevamente, pero ahora “arg3=10”
Se obtiene como resultado:
Como se observa, dado que el precio de las manzanas aumenta el individuo ahora comprará más naranjas que manzanas; sin embargo, como su ingreso no ha aumentado, comprará menos manzanas que en el ejemplo1.
(Para mayor visualización de la imagen, hacer click en la misma)
Elaborado por: Iván Límaco

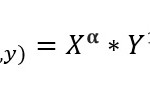
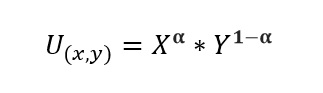
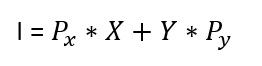
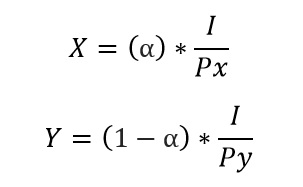
11/09/2014 a las 7:00 pm
La maximización de la utilidad del consumidor es un problema clásico en microeconomía. Plantearía el caso para tres bienes, por ejemplo naranjas, manzanas y plátanos, tendriamos entonces que:
La función de utilidad: U = X^alpha * Y^beta * Z^gamma
sujeta a la restricción presupuestaria ingreso: I = Px + Py + Pz.
Hay que hacer la optimización aplicando las condiciones de primer orden KKT y en el visual basic se tendría más argumentos:
arg1: alpha
arg2: beta
arg3: gamma
arg4: I: ingreso
arg5: Px: precio naranjas
arg6: Py: precio manzanas
arg7: Pz: precio plátanos
Function CantidadOptimaConsumida(arg1, arg2, arg3, arg4, arg5, arg6, arg7)
Resultado = (el algoritmo que resulta de la optimización)
Utilidad = Resultado
MsgBox “La cantidad consumida del bien es ” & Resultado
End Function
11/09/2014 a las 7:02 pm
En el ejemplo anterior se usó para la función utilidad del consumidor una función Cobb Douglas.
15/02/2015 a las 10:51 pm
De la misma forma, considero que es posible utilizar este método para calcular otros temas vistos en microeconomía como Demanda de trabajo de acuerdo a la siguiente función:
F(L,K,H) = (AL^α1)*(K^α2*)*(H^1-α1-α2)